Ao ingressar na escola de engenharia, com o segundo lugar no vestibular, eu era um jovem com boa formação – mas completamente tonto em termos de orientação vocacional.
Meses antes, eu hesitava entre ser jornalista ou veterinário.
Ao final do primeiro ano da escola, estava decepcionado com o excesso de teoria, e com a pouca noção da utilidade do que estava aprendendo.
Eu trabalhava como desenhista numa fábrica de estruturas metálicas e de mecanismos para a construção civil, e por isto, optei por seguir um curso de engenharia civil e mecânica. Este formato não existia. Como nesta época eu brincava, em casa, com alguns experimentos elétricos, resolvi ser civil-eletricista. O curso duplo me ampliava o leque, eu ainda não sabia bem o que queria…
À medida que avançava no curso, e em paralelo com os empregos que eu conseguia, como estudante, comecei a pender para a engenharia civil, em especial para o cálculo estrutural.
Meu primeiro emprego tinha sido de locutor em rádio, no horário da madrugada; o segundo, foi fazer desenhos a nanquim, para acompanhar as propostas de estruturas metálicas da Bonaspetti Ltda.
O velho Bonaspetti era um engenheiro calculista, muito experiente, tinha trabalhado no Itália e no Peru.
Lembro que um dia, sai para almoçar, com um desenho pela metade. Já estava todo rasurado (tinta nanquim sobre papel vegetal), borrões mal disfarçados, o papel fino, em alguns lugares, de tanto ser raspado com a gillette…
Eu fizera o meu melhor, mas estava muito preocupado com a qualidade que estava conseguindo – e com tempo que estava levando!
Quando voltei do almoço, o desenho tinha sido refeito, numa folha limpa: estava pronto, e perfeito.
Fiquei perplexo, e desolado. O velho tinha feito tudo, no intervalo de almoço!
– “Poco a poco, poco a poco” me murmurou ele, de forma carinhosa, sentindo o meu desapontamento…
Palavras que nunca esqueci, evitaram que eu desmoronasse, naquele momento tão importante da minha carreira de futuro engenheiro….
Na faculdade eu continuava aprendendo teoria, com professores que considerava, muitas vezes, medíocres.
No escritório, quando o engenheiro Luz saía, eu ficava tentando entender os cálculos que estava fazendo.
Um dia, finalmente, a grande recompensa. Ele dimensionara as terças de uma estrutura com U de 4 polegadas; eu refiz o cálculo, seguindo um roteiro que tinha copiado do velho Bonaspetti. O U de 3 passava! Deixei um bilhete para o engenheiro Luz.
No dia seguinte, a resposta, em outro bilhete: ele me elogiava pelo esforço, e tinha alterado o projeto.
Anos depois, já fanatizado no aprendizado da gestão pela qualidade, aprendi que aquele tinha sido um importantíssimo ZAPP! para minhas indecisões vocacionais…
Finalmente, no terceiro ano da escola, começamos a ver alguma coisa prática. Numa aula do professor Eládio Petrucci aprendi o que era o momento fletor, o qual, na prática, eu já utilizara dois anos antes, no caso do U de 3…
Eu bebia aquelas aulas com um entusiasmo difícil de descrever e de explicar.
Eu ia ligando fatos reais, da ciência das construções, com vivências que eu tivera, cheio de curiosidade e incertezas.
Eu sentida que, finalmente, estava começando a ser um engenheiro!
No quarto ano, finalmente, a cadeira de concreto armado. Eu estava tão motivado, que acordava de madrugada para ler trechos do livro do Langendonck, antes de a matéria ser dada!
Didaticamente, o livro era um porre. Tinha notas de rodapé tão extensas, que ocupavam páginas inteiras!!! Mas eu queria saber e, principalmente, queria enfrentar o professor da matéria, cuja falta de didática e de comprometimento com o que fazia, me revoltava, a cada aula.
Eu estava louco para aprender, a competência e atitude do mestre eram um antídoto extremamente poderoso.
Quando eu cheguei ao quinto ano, já comecei a trabalhar como calculista, dimensionando estruturas de concreto para prédios de poucos pavimentos.
Quem me deu a primeira oportunidade foi um engenheiro jovem, que gostava mais da parte de obras, e revisava – e assinava – os cálculos que eu fazia.
Ele me perguntara quanto eu queria ganhar por hora. Eu propus que, quando eu entregasse o trabalho, ele avaliasse o tempo que outro levaria, e me pagasse o que considerasse justo.
Na realidade, eu era muito rápido, no cálculo. Desenvolvia ábacos de apoio para ganhar velocidade, e, com este tipo de contrato, ganhava, por hora, 40 a 50% mais do que o preço corrente na ocasião…
O Henri fazia muito prédios de até 3 andares (não precisava de elevador), e a qualidade do tijolo gaúcho permitia que não fossem necessárias vigas entre andares.
Assim, as vigas de baldrame – aquelas que transferiam todo o peso da estrutura às sapatas de fundação – era calculadas para suportar o peso de todos os andares que estavam por cima.
Numa “Enciclopédia Técnica Universal”, editada pela Livraria do Globo, de Porto Alegre, descobri que havia uma norma alemã que permitia reduzir bastante a carga que incidia sobre as vigas mencionadas.
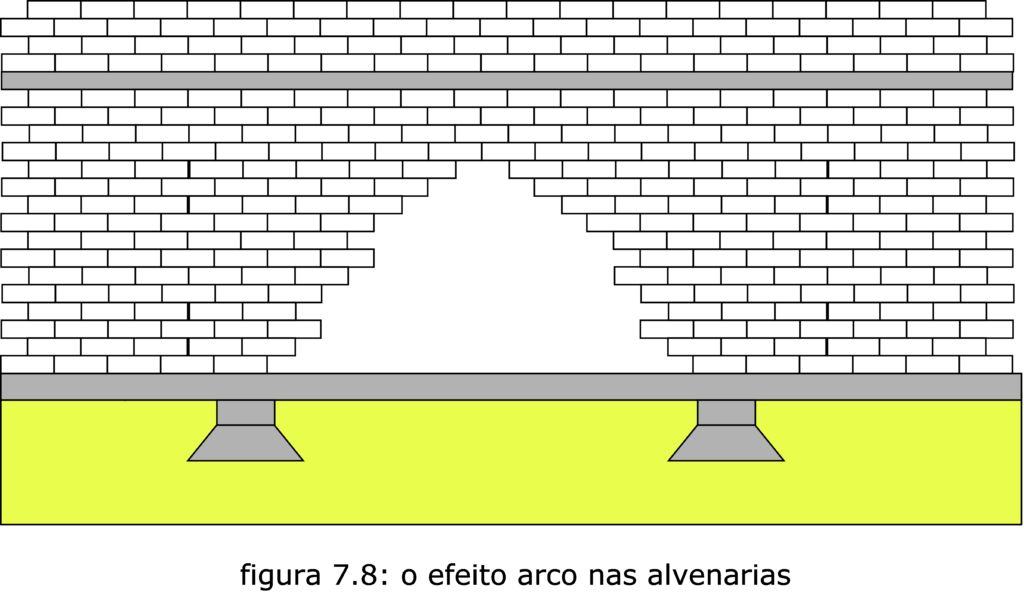
O princípio era bem lógico: se removemos um arco de tijolos, o resto da parede não cai; logo, o que pressiona a viga de baixo é, apenas, o peso deste arco! (fig. 7.8)
A lógica era aceitável, a norma era alemã. Não tinha por que não usar este novo conhecimento, que, assim, chegava a Porto Alegre…
Dali por diante, todas as vigas de baldrame dos prédios do Henri eram mais baratas do que as dos seus concorrentes…
Ainda como estudante calculista, tive ocasião de participar da emoção da aplicação de outro conhecimento absolutamente novo em nosso meio.
Foi no cálculo da estrutura de um hotel, com doze andares, e com apenas 2 colunas, numa de suas dimensões. Era uma verdadeira fatia de queijo.
Outro calculista tinha calculado todas as vigas e lajes, mas tivera receio de calcular as colunas.
É que, na sustentação de um prédio com esta configuração, contra a força do vento, as colunas funcionam em conjunto com as vigas, como um pórtico múltiplo (linhas mais cheias da figura 7.9).

Não havia computador, na época, e o usual era utilizar o método de Cross, que era extremamente trabalhoso. Não me parece possível explicá-lo em poucas linhas. O método era interativo, para um prédio deste tipo se precisavam efetuar muitas centenas de cálculos, até chegar ao resultado final. E havia o risco de, ao longo do processo, se cometer um erro, o que poderia, evidentemente, afetar o resultado final.
O engenheiro Percy Abreu, de quem eu fora desenhista, alguns anos antes, tinha traduzido uma apostila que explicava um novo método de calcular este tipo de estrutura.
O método de Canning tinha algumas características que parecem inverossímeis:
- erros cometidos ao longo do trabalho não afetam o resultado final, só o retardam;
- qualquer pessoa com boa habilidade em contas pode fazer as interações, horas a fio – mesmo sem nenhum conhecimento de cálculo estrutural;
- quando entrega o trabalho, em poucos minutos podemos verificar se o resultado está certo;
- entretanto, não se chega ao resultado final – que sabemos conferir – sem que o trabalho exaustivo tenha sido feito;
- se fizermos boas estimativas iniciais, intuindo o funcionamento da estrutura, o processo de cálculo demora menos tempo.
Perfeito. Dei as instruções para meu irmão menor, que estava numa fase de paixão pela matemática. Ele fez as interações do primeiro pórtico, levou alguns dias calculando. Com a conferência, eu já tinha idéia de como se comportaria o segundo, e assim o cálculo deste levou bem menos tempo.
É um caso em que o conhecimento de um método, na tecnologia do negócio, representou, para mim, uma inovação – e uma solução brilhante para um problema real que eu tinha.
Além do uso deste novo método de cálculo, eu consegui reduzir as dimensões das colunas fazendo com que seus eixos não estivessem exatamente numa mesma vertical.
Era uma proposta lógica, mas que eu nunca tinha visto.
Conferi com dois professores da faculdade, tive o nada-obsta, e economizamos um bocado de concreto na estrutura do hotel…
Mais adiante, me dei conta de que, no cálculo de concreto armado, a gente só sabe se acertou quando analisa falhas em estruturas.
– “O concreto é o melhor amigo do homem” me diziam.
– “É preciso caprichar no cálculo de marquises e de caixas d’água” – me ensinaram.
– “A marquise, por que, se fizeres um erro, o resto da estrutura não a socorre, ela vem abaixo. E a caixa d’água porque a carga que assumiste, realmente acontece. Não é como ponte, ou prédio, em que raramente a carga máxima ocorre. Na caixa d’água a carga máxima está lá, todas as horas, em todos os dias…”
Quando aparecem rachaduras nos prédios, é que vai se entender como a estrutura realmente funciona.
E foi baseado nesta realidade que, nos anos sessenta, começaram a aparecer teorias de cálculo revolucionárias, sob a denominação de método da ruptura.
A mudança de conceito era lógica, e prática.
Normalmente, se parte de uma configuração de cargas, se calculam as tensões que ocorrem no interior das peças da estrutura, e se compara estas tensões com as que aquele material é capaz de resistir – com um fator de segurança previsto nas normas.
Na prática, se uma viga de um prédio vier a fissurar numa ponta, o prédio não cai: o outro lado da viga fica sobrecarregado, a laje ajuda um pouco e, no fim, a estrutura toda se acomoda.
Esta acomodação é o que não ocorre nas marquises – e é por isto que elas caem tanto.
Como o colapso de uma estrutura hiper-estática só ocorre no conjunto, e não na falha da primeira peça, os métodos da ruptura passaram a considerar este efeito, e invertiam o processo de cálculo.
Passou-se a definir, pelo dimensionamento, o limite de resistência das peças, calculando depois a carga que o conjunto sustenta, quando a última peça falhou. O coeficiente de segurança incide sobre a carga total.
Este método permitiu grande economia nas estruturas, e simplificou muito o cálculo, tornando dispensáveis muitas das exaustivas interações sobre as quais discorremos antes.
Tive a felicidade de participar da introdução deste novo conceito de cálculo em nosso meio, e da gradual descoberta das inúmeras situações em que ele representava soluções melhores para as tarefas que tínhamos que realizar.
Resolver problemas reais com soluções inovadoras era, para mim, motivo de enorme prazer.
Mas a vida do calculista é dura.
A gente passa horas a fio fazendo contas.
Meu colega Edson Garrastazu de Almeida, anos depois, me disse que também abandonara o cálculo, por que, com o tempo, “a gente calcula até o tempo que leva para cuspir”…
Na realidade, eu decidi interromper a minha paixão por esta área quando me dei conta de que estava caminhando olhando para o chão, não conseguia olhar as pessoas na rua.
De tanta concentração no trabalho, eu estava me tornando excessivamente introspectivo.
Bons tempos, bom mercado de trabalho, em que nos era permitido mudar de profissão, ainda em tempos de faculdade…
A paixão pelo cálculo deixou sequelas.
Quando estava no último ano da faculdade, o Percy Abreu me convidou para ser seu assistente na cadeira de Resistência dos Materiais, na PUC.
Foi outra experiência muito importante. Assumi o cargo de titular da cadeira logo em seguida, pois o Percy se tornara executivo, não mais era um calculista de concreto, e teve que atender a outros compromissos.
Lecionei durante 6 anos, sem que, em nenhum momento, alguém mais experiente viesse verificar minhas aulas, discutir a matéria que eu estava dando, conferir minha didática…
Mas a base que adquiri naqueles anos de paixão juvenil vieram a se revelar muito úteis, ao longo da minha vida profissional.
O fato de ter lecionado Resistência dos Materiais me obrigou a estudar com muita profundidade esta matéria, na qual atingi um domínio muito sólido em conceitos.
O que me foi útil em muitas ocasiões.
Quando precisei entrar em projetos que normalmente são conduzidos por engenheiros mecânicos, iniciei pela área de tubulações industriais.
E logo descobri que havia um problema mal resolvido.
Quando as tubulações aquecem ou esfriam, a sua dilatação / contração é capaz de causar enormes esforços sobre as paredes dos tubos e sobre as estruturas que as sustentam.
E os engenheiros mecânicos, via de regra, não são muito bons em cálculos estruturais, e quando calculavam flexibilidade de tubulações, usavam simplificações e tabelas muito grosseiras, a favor da segurança, que produziam soluções muito onerosas.
Era uma oportunidade de agregar valor, ganhar respeito de colegas de outra área. Pois eu não apenas um aprendiz; eu também era capaz de trazer conhecimento útil para o projeto.
Apliquei técnicas do método de Cross e do cálculo de concreto na ruptura para descobrir que os esforços da dilatação sobre as fundações, em muitos casos, eram ordens de grandeza inferiores aos que eram correntemente calculados.
A partir deste ponto, passei a ser aceito como um membro da confraria dos conhecedores da área…
 ]]>
]]>

